Filling in Notes
technique

In this Sudoku Academy tutorial, we’ll focus on preparing for elimination strategies by filling in notes or potential candidates in empty cells. 

As a general rule, we progress in Sudoku games by placing numbers until we reach a point where no further progress can be made. The next step involves determining possible candidates for empty cells. Filling in notes will help identify opportunities for elimination.

With notes, fill in all possible candidates for each empty cell, considering the numbers already placed on the Sudoku board. But be aware that placement accuracy is crucial. Mistakes can make the game more difficult and time-consuming. 

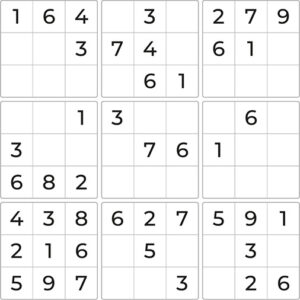
Let’s examine the third and highlighted column. It has two empty cells. Analyzing both the row, column, and block of each cell we can easily see that only 5 and 9 are possible candidates. Let’s fill in the notes. 

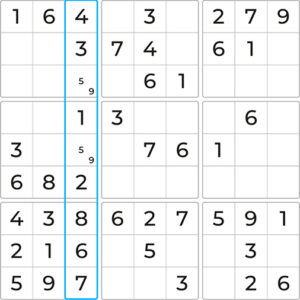
Moving on to the fifth and highlighted column, we can see that candidates 1, 8, and 9 are missing. However, this time we need to be more careful. The highlighted cell prevents 1 as a candidate in the first empty cell. Let’s fill in the 1s in the last two empty cells. In turn, the highlighted cell containing 8 prevents it from being placed in the 2nd empty cell. And the highlighted cell containing 9 prevents it from being a candidate in the last row. Filling the notes highlights that in the middle block, the 9 can only be placed in two cells.

If we highlight the 9s already placed in the 8th and 9th column, then we can easily see that the 9 in the 7th and highlighted column can only be placed in the 4th and 6th row. 

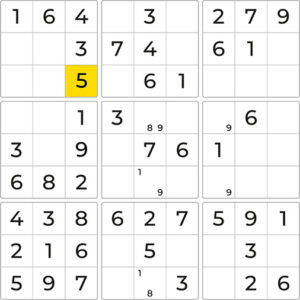
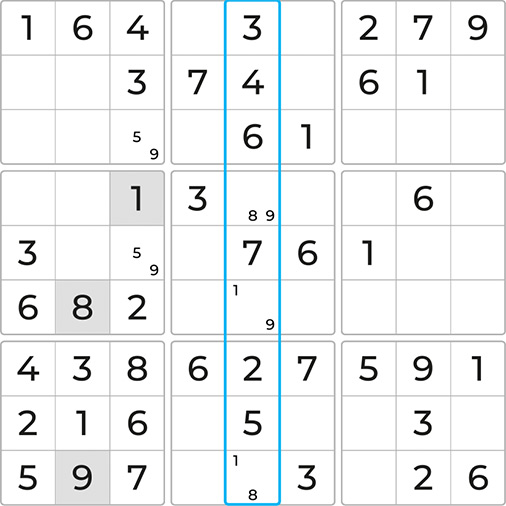
But wait! What about the middle row? Where does the 9 go? Turning to the middle block on the left we can easily see that the highlighted cell prevents 9 as a candidate in the 2nd column only leaving the third column as an option. We can now place the 9 and by placing the 9, we can also place the 5 completing the third column.

Prefer solving over manual note-taking? We’ve added a great feature: auto-filling all possible candidates. Just tap the designated button, and all possible candidates are filled automatically—like magic!

Now that all possible candidates are placed, we can apply similar logic to what we have just learned. In the middle block, the 9 can only be placed in the middle column. As a consequence, the other 9s can be eliminated. This leaves a so-called Hidden Single in the middle row, where the 9 can only be placed in the highlighted cell. Continue placing the 9 and 5 accordingly.

Elimination techniques in Sudoku often reveal Hidden Singles, though they’re not always easy to spot. Pay close attention, as they appear at various stages of the game.

Be sure to watch the video for additional elimination techniques on your path to becoming a Sudoku Master! Practice your skills with Sudoku X, and master beyond beginner and easy gameplay.

Locked Pairs/Triples
technique

Let’s continue in this Sudoku Academy to build on the foundational skills acquired from the beginner to medium-level series on placement strategies. This and the next tutorials will focus on basic elimination techniques to be applied when placement strategies don’t allow further progress. These techniques can be practiced by playing our hard level games. 

Let’s look at an example. Starting with a classic Sudoku board, we solve the game as far as we can by placing numbers using basic placement techniques. However, at some point, we cannot progress further. Filling in notes is the next step, allowing us to look for elimination opportunities.

We refer to our tutorial on adding notes to the board. In any case, if you want to spend your time solving rather than manually filling notes, then we have added a great feature for you and that is auto-filling the notes. Just tap the designated button and all possible candidates are filled automatically. Magic!

The art of the Locked Pairs technique is to search for two cells containing the same two numbers. These two cells are confined to two houses, either a row and block or a column and block. When a locked pair is identified, the same two numbers can be eliminated from other cells in the same houses.

Turning to the block in the top center, we can see two cells in the same row, both containing only the numbers 1 and 6. This is a typical example of Locked Pairs, and with candidates 1 and 6 locked, these can now be eliminated from other cells in both houses. In our example, the number 1 can be eliminated from cells in the same row to the right. Great!

Although we have progressed closer to solving our Sudoku, we are not yet able to place another number.

So let’s turn to the block in the bottom center. Analyzing the block, we can observe a Locked Triple. The candidates in the three cells on the left are confined to the same block and column, limited to the numbers 1, 5, and 9. As only three numbers are possible, the same candidates can, in turn, be eliminated from the other cells in the same block. This time, eliminating number 1 results in a single possible candidate that can be placed. Place the 6 and continue solving your game.

Locked Pairs and Triples are elimination techniques that can be frequently applied to solving Sudoku games. Make sure to also watch our videos featuring other more advanced or basic elimination techniques on your journey to becoming better and better. Practice your skills with Sudoku X and master the hard levels and beyond.

Naked Pairs/Triples
technique

We will continue in this Sudoku Academy to build on the foundational skills acquired from the beginner to medium-level series on placement strategies. This tutorial focuses on elimination techniques to be applied when placement strategies don’t allow further progress. These techniques can be practiced by playing our hard-level games.

Let’s look at an example. Starting with a classic Sudoku board, we solve the game as far as we can by placing numbers using basic placement techniques. However, at some point, we cannot progress further. Filling in notes is the next step, allowing us to look for elimination opportunities.

We refer to our tutorial on adding notes to the board. In any case, if you want to spend your time on solving rather than manually filling notes, then we have added a great feature for you and that is auto-filling the notes. Just tap the designated button and all possible candidates are filled automatically. Magic!

The Naked Pairs and Triples solving technique is similar to its Locked equivalent. The art of the Naked Pairs technique is to search for two cells containing the same two so-called candidates. However, unlike the Locked equivalent, these two cells are only confined to one house, a row, a column or a block.

Turning to the sixth row, we can see two cells both containing only the numbers 4 and 6. This is called a Naked Pair. With two cells only having two candidates, we can now eliminate candidates 4 and 6 from other cells in the same row. This reveals another pair with candidates 1 and 3 in the same row.

Although we progressed, we are still not able to place a number. But hold on… if we turn to the center column, we discover that this column holds a Naked Triple in the cells of rows 1, 3, and 6.

These cells combined only have 3 candidates that can be placed in them, allowing us to eliminate the numbers 1, 3, and 6 from the other cells in the same column. This reveals number 8 in the last row which can in turn be placed allowing you to progress and solve the Sudoku board with placement techniques. Nice!

The Naked Pairs and Triples techniques are elimination techniques that can be frequently applied to solving Sudoku games. Make sure to also watch our videos featuring other more advanced or basic elimination techniques on your journey to mastering Sudoku. Practice your skills with Sudoku X and excel at the hard levels and beyond.

Pointing Pairs/Triples
technique

In this tutorial of the Sudoku Academy, we will introduce you to an elimination technique called Pointing Pairs. 

Pointing Pairs is a frequently used technique in solving Sudoku games. Its Triple equivalent is less common. However, the elimination logic works in the same way. If within a block all candidates of a certain number are confined to a single row or column, following the basic Sudoku rules, that number cannot appear in the same row or column outside of that block.

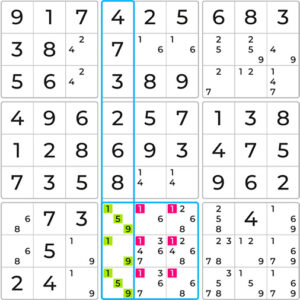
Consider the first row and block in the top-left corner. The empty cells within the block that hold candidate number 6, are confined to the first row. As number 6 should appear once in the block, we can safely eliminate all other possible 6s from all cells outside the block within the same row. 

Since we are not yet able to place any numbers, let’s continue analyzing the second column. In the middle-left block we can observe that candidate number 1 can only be placed in the second column. Applying the same elimination logic, all number 1 candidates outside the block in the same column can be eliminated.

Block-Line Reduction
technique

In this tutorial of the Sudoku Academy, we will introduce you to an elimination technique called Block-Line Reduction. 

Block-line reduction is a frequently used technique in solving Sudoku games. Compared to Pointing Pairs, the elimination logic is the other way around. With Pointing Pairs candidates are eliminated within the row or column outside the block. With the Block-Line Reduction technique candidates are eliminated within the block itself. An opportunity for elimination arises when all candidates of a certain number within a row or column are confined to cells within a single block. If so, the candidate can be eliminated from all other cells within that same block.

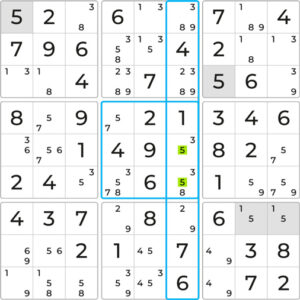
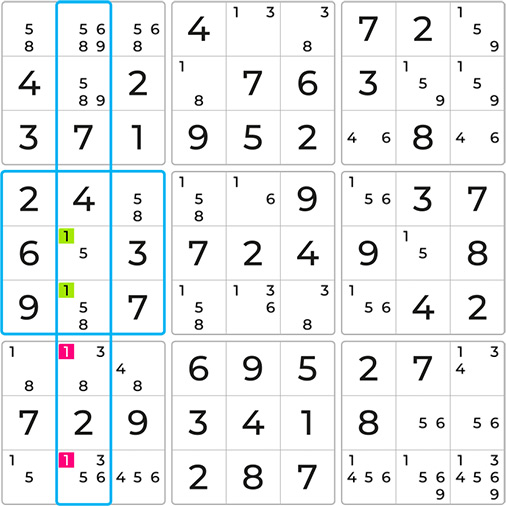
Let’s analyze a Sudoku puzzle with filled notes. Consider the middle, highlighted block, and the 6th, highlighted column. Let’s investigate candidate number 5. In the first row, 5 is already placed in the highlighted cell, so it doesn’t qualify as a candidate in the highlighted column. Similarly, in row 3, 5 is already placed in the highlighted cell. In row 7, we can observe a Naked Pair of 1 and 5 in the two highlighted cells. Although we don’t know the exact cell yet, 5 must be in one of them, eliminating it as a candidate in the same row and highlighted column.

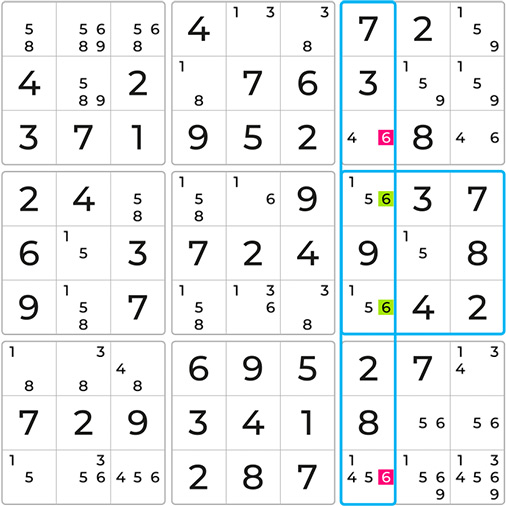
This leaves only the 5s in the middle block, highlighted in green, as possible candidates for that column. 

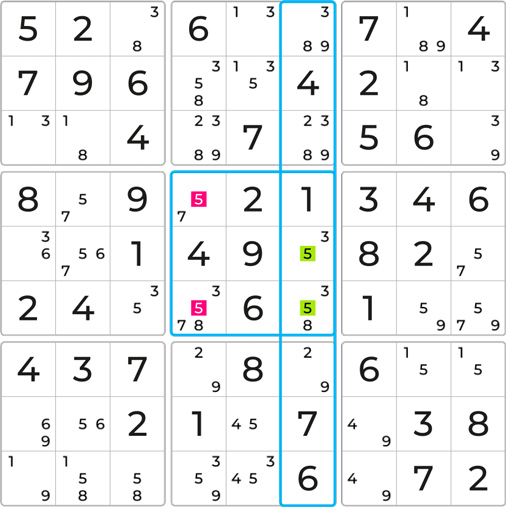
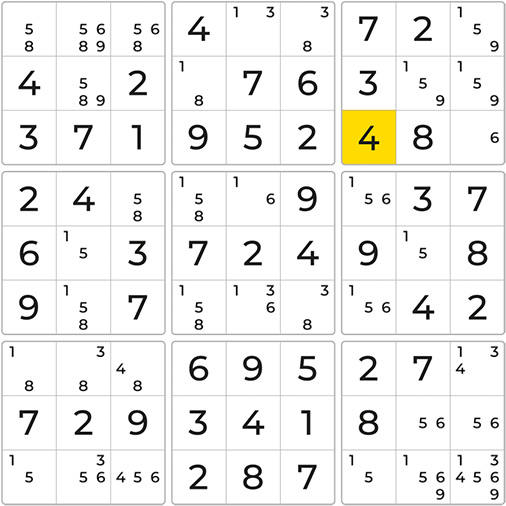
Since the 5 must be placed in one of the two cells, all other 5s in the same block can be eliminated. This enables the placement of 7, allowing you to continue solving the game. An example of Block-Line Reduction. Super!

On your journey to becoming a Sudoku master, don’t forget to check out our other video tutorials covering both basic and advanced elimination techniques. Enhance your skills by practicing with Sudoku X, which offers challenging gameplay that will push your abilities to the limit.

Hidden Pairs-Triples
technique

In this tutorial of the Sudoku Academy, we will introduce you to an elimination technique called Hidden Pairs and Hidden Triples.

The Hidden Pairs and Triples elimination techniques operate similarly, with the main distinction lying in the number of cells and candidates involved. In the context of Hidden Pairs, the aim is to identify two cells within a row, column, or block that contain two candidates each. These candidates cannot be placed in any other cell within the same house other than those two cells. Consequently, any other candidate present within those two cells can be eliminated. This Sudoku technique differs from the Naked equivalent in that it eliminates other possible candidates within the two cells.

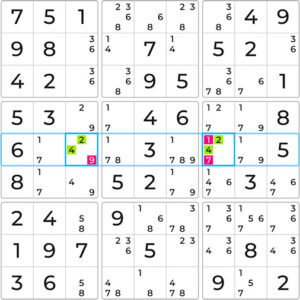
As an illustration, let’s examine the middle row of a Sudoku board with all notes filled in. By analyzing the possible placements of all candidates, we observe that the numbers 2 and 4 can only be placed within the highlighted cells. Since there are only two possible candidates for two cells, we can confidently eliminate all other candidates from those cells. This is another step in solving the Sudoku puzzle. Nice!

We cannot place numbers yet, so we must continue searching for elimination opportunities. Let’s focus on the fourth highlighted column. By analyzing the possible placements of candidates, it becomes clear that the numbers 2, 3, and 6 can only be placed into three cells within that column. We have found ourselves a Hidden Triple! This allows us to eliminate the number 8 from the cells in the first and third row. 

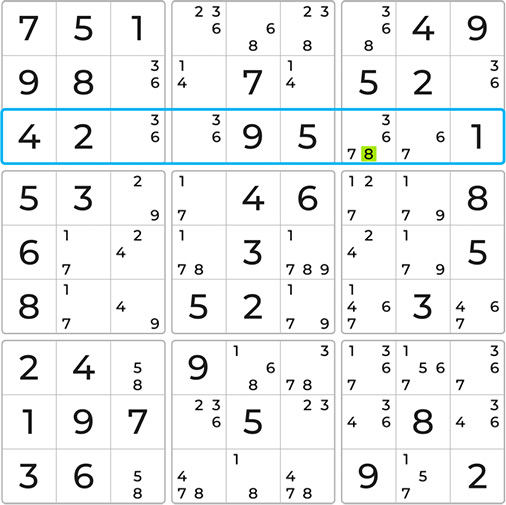
Now, staying with the third and highlighted row, we can see that the number 8 can only be placed in the highlighted cell. This is called a Hidden Single. Let’s place it and proceed to solve the Sudoku board further. Cool!

Unlike its Naked equivalent, a Hidden Single, Pair, or Triple can be more challenging to identify. When making mistakes while filling in notes, it is likely to get stuck in finding the solution. To prevent getting stuck, Sudoku X offers the auto-fill notes option, which allows users to concentrate on solving the puzzle while the app helps to fill in the notes accurately.

Be sure to watch other videos for additional elimination techniques on your path to becoming a Sudoku Master! Practice your skills with Sudoku X and master beyond beginner and easy gameplay.

Naked Quad
technique

Welcome to the Sudoku Academy by Sudoku X, where we build upon the foundational skills acquired at beginner levels. In this tutorial and beyond, you’ll learn intermediate strategies that bridge the gap between easy and hard gameplay. In this tutorial, we will introduce you to an elimination technique called Naked Quads.

The Naked Quads technique works in exactly the same way as its Naked Pairs and Triples counterparts, however it involves four candidates in four cells. Naked Quads are rarer and more challenging to spot.

Let’s examine a Sudoku board with the notes already filled. If we focus on the last four empty cells in the highlighted row, we observe that only four candidates — numbers 4, 5, 7, and 9 — can be placed in these cells. Since these four candidates are confined to exactly four cells, we can eliminate them from all other cells in the same row.

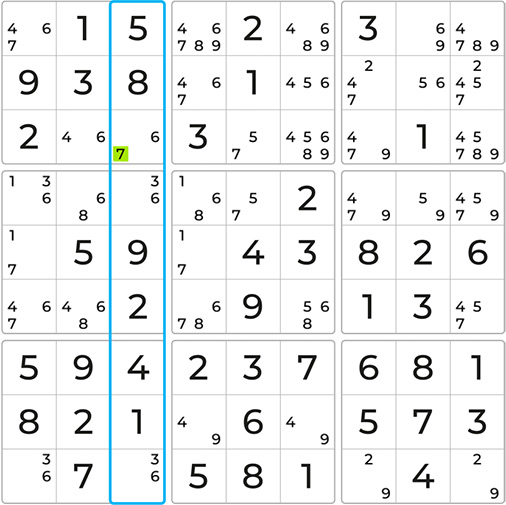
Now that we have eliminated candidate 7 in the highlighted column, a Hidden Single is revealed. This allows us to eliminate candidate 6 in the highlighted cell, and confidently place the number 7. We can now continue solving our Sudoku game.